Weight
It is helpful to explore two terms that are often used interchangeably in common language: ‘mass’ and ‘weight’.
Consider a person, equipped with roping gear and tools, has a total mass of 100kg. Mass is defined by volume and density and these two factors will not change for this 100kg person.
One of the biggest myths that we are taught from a young age is that our ‘weight’ is measured in kilograms (or pounds). While this is fine for most daily situations, it is a significant barrier for those wishing to progress with an understanding of rigging physics.
Weight describes the force that a mass, influenced by gravity, applies to a surface and it is measured in Newtons (N).
The weight that a person applies to the surfaces we encounter in everyday life is a result of the gravitational pull towards the center of our earth. We quantify this force by multiplying the mass (100kg) by the acceleration it would experience towards the center of the Earth if our surface was not present. This rate of acceleration is normally assumed to be 9.81 meters per second per second, or 9.81m/s², and is typically denoted as g.
Force = mass x acceleration, or:
So, Weight = mass x acceleration due to gravity, or:
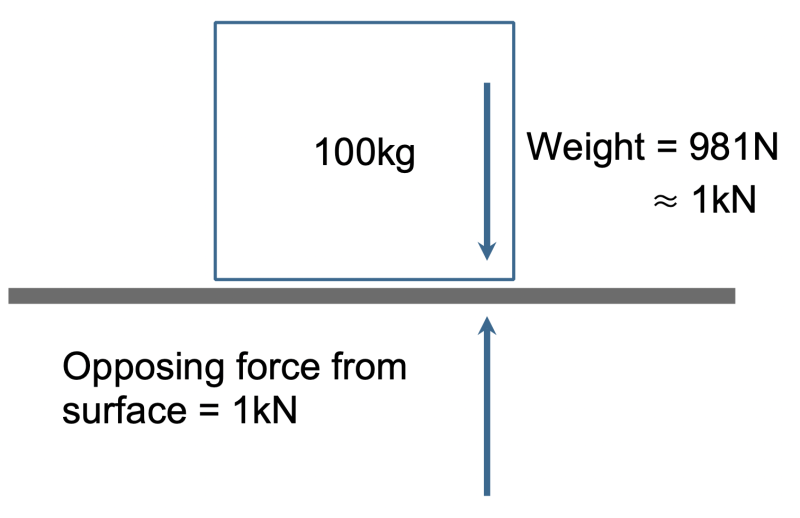
Therefore, in this instance, the weight of a 100kg block of steel is:
W = 100kg x 9.81m/s²
W = 981 kgm/s² or 981 Newtons
To simplify this for in-the-field calculations we make the approximation that g ≈ 10m/s² and get:
W ≈ 100kg x 10m/s²
W ≈ 1000N or 1kN
For an object, such as our 100kg steel block, to remain stationary we can consider that the forces acting on it are all balanced and therefore present a state of equilibrium. Note that, to represent forces of equal magnitude but opposite direction, the two forces in the drawing above are shown as equal length vectors with arrows denoting the direction of application.
In practice, a typical aluminium screw-gate carabiner will be marked “<-> 30kN”. This means that it should be able to support a stationary suspended mass of (30,000N ÷ 10m/s² =) 3,000kg.
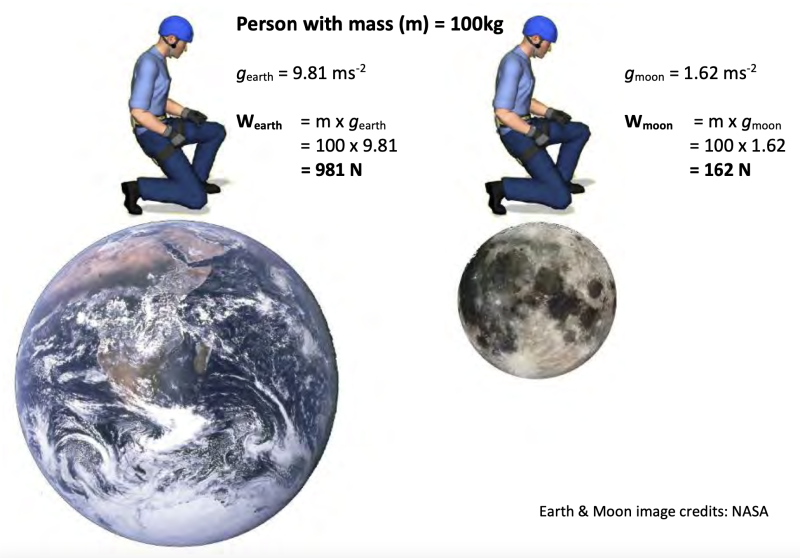
Because weight is a function of gravity, the weight of a particular mass will vary according to the local gravitational field, so it would ‘feel’ lighter on the moon.