Vectors
There are two important distinctions we make in quantifying attributes assigned to objects – some need a simple quantity (a ‘scalar’ value) whereas others need both the magnitude and direction described by a ‘vector’.
Some common terms confuse this distinction but, for example, technically there is a significant difference between ‘speed’ and ‘velocity’. Speed is a scalar value and simply describes how fast something is going whereas velocity is a vector and adds a direction to the ‘how fast’. A car may have a speed of 60km/h but we could describe its velocity as 60km/h heading 45degrees true north.
If we want to purchase one apple worth for 1.00 and one orange worth 0.50 then, given that currency is a scalar value, we simply add these to get 1.50.
If we were at the back of a train traveling at 60km/h heading true north and then we were to run towards the front of the train at 10km/h, our velocity (relative to the ground) would be 70km/h true north.
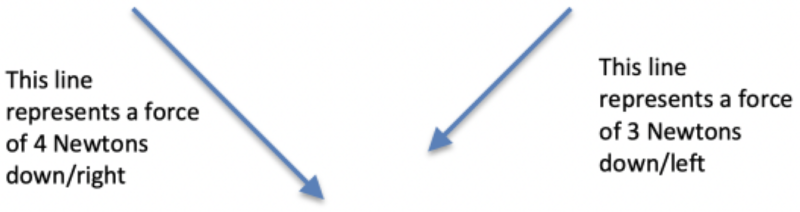
If we represent the magnitude and direction of a force with a line where the length of the line is proportional to magnitude and the arrow defines direction, then we could draw two forces as follows:
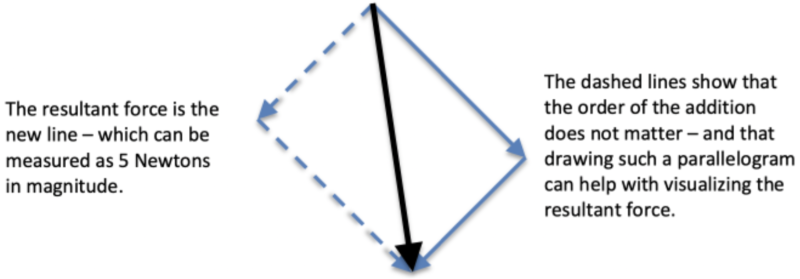
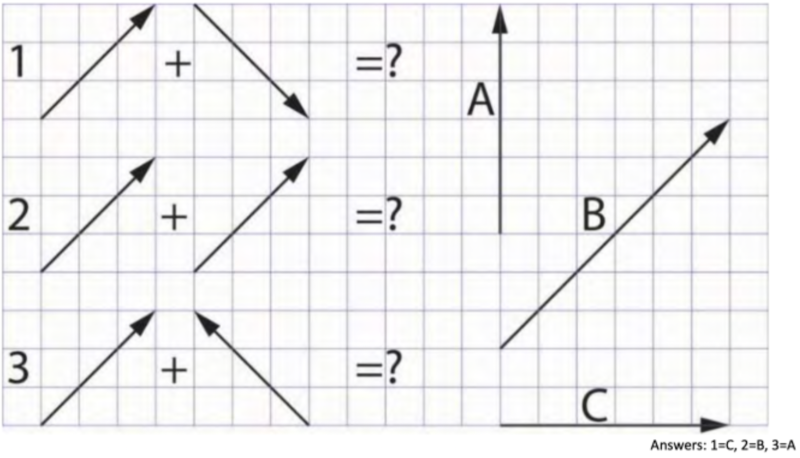
If the forces are applied to an object, whether they are applied one after the other, together, or in the reverse order, the net result will be the same.
To determine the result of adding these forces, one of these lines needs to be moved so that its tail is positioned on the head of the other – and the sum is a new line from the tail of the first to the head of the second: