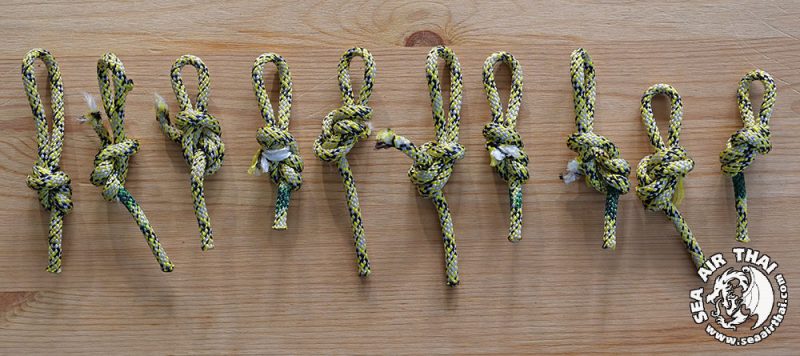3 Sigma
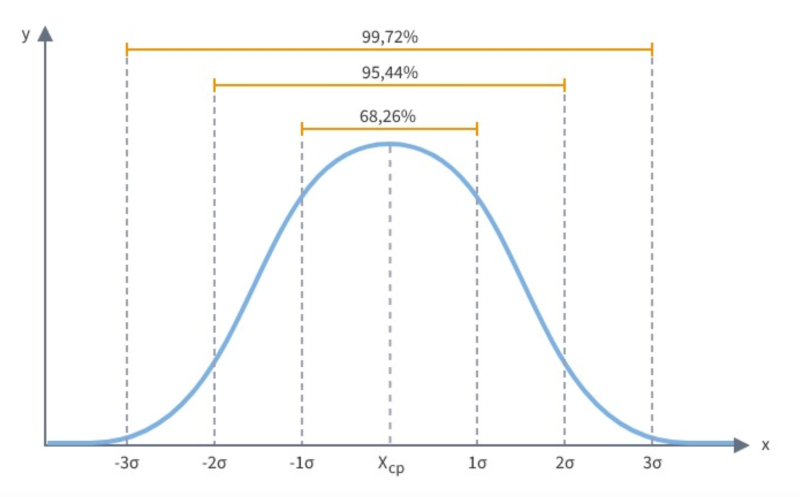
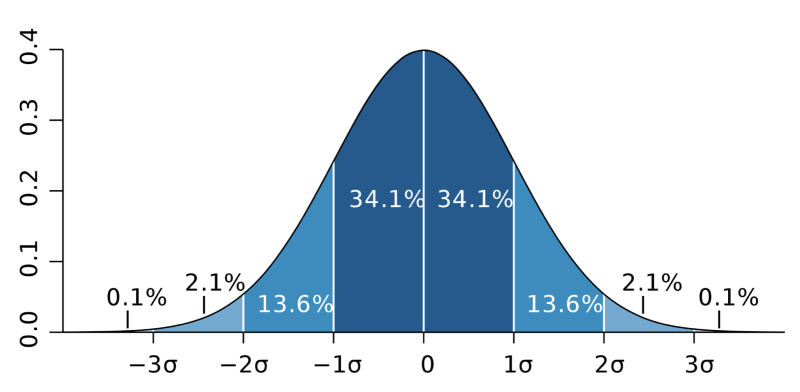
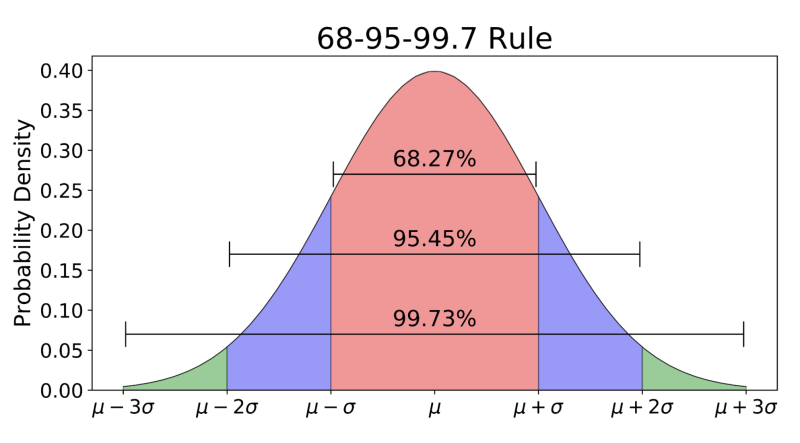
3 Sigma (3σ) is a statistical formula used to calculate probability. It is commonly used for computing the minimum breaking strength (MBS) of Climbing, Rope Rescue, and Rope Access equipment. Using the 3 Sigma formula provides a way to determine a safe minimum breaking strength from a range of numbers gathered during testing. When used to calculate the minimum breaking strength it gives confidence that the minimum breaking strength is higher than 99.7% of samples tested.
The three-sigma process:
- Carry out at least 5 breaks of the item to be rated
- Calculate the mean
- Calculate the standard deviation
- Multiply the standard deviation by 3
- Subtract the product in step 4 from the mean
The simplest way to explain 3 Sigma is to show how it is computed. For this example we broke Figure 8 knots tied in Teufelberger 6mm Nodus Accessory Cord and recorded the results on a Rock Exotica Enforcer Load Cell.
Ten tests were conducted with the following results recorded in KiloNewtons (kN):
- Test #1: 7.20 kN
- Test #2: 7.97 kN
- Test #3: 6.57 kN
- Test #4: 6.84 kN
- Test #5: 6.44 kN
- Test #6: 7.49 kN
- Test #7: 6.92 kN
- Test #8: 7.38 kN
- Test #9: 6.51 kN
- Test #10: 6.96 kN
10 tests resulted in the knot breaking within the range of 6.44 kN – 7.97 kN.
The first step in computing the 3 Sigma value is to compute the mean breaking strength which comes out to 7.03 kN.
The next step is to compute the standard deviation. The standard deviation is the amount of variation in a set of values. If all the numbers are very close to the mean then the standard deviation will be a small number. If there is a wide range of numbers further away from the mean then the standard deviation will be a larger number. The smaller the standard deviation in a set of values the higher the quality of manufacturing.
For the results of this test the standard deviation is computed as 0.49 kN. Since we are computing a 3 Sigma value we multiply the standard deviation by 3 resulting in 1.47 kN (0.49 kN * 3).
This value is then subtracted from the mean resulting in a final 3 Sigma value for this test of 5.56 kN (7.03kN – 1.47 kN).
Using 3 Sigma gives confidence that although there is still a 0.14% chance of the knot breaking lower than 5.56 kN the chance is very small. This number can be made more accurate by increasing the sample size. Instead of 10 tests, 20 or even 50 could have been performed. The more tests that are performed, the more confidence we have that this number is truly representative.
Note that the 3 Sigma number computed for this test, 5.56 kN, is 13.66% lower than the lowest recorded value, 6.44 kN. What if the lowest obtained value, 6.44 kN was used instead for the minimum breaking strength? In this case, we would expect 11.35% of values to fall below 6.44 kN. More than 1 out of 10 would be below the rated strength. When the 3 Sigma number is used instead, only 1 out of 715 will fail below the rated strength.
Minimum Breaking Strength is very different from Average Breaking Strength (ABS), although, abs is used in the calculation of MBS.
Sterling applies three-sigma testing for MBS to our standards because it is much more rigorous and therefore safer than using simply the Average Breaking Strength.
- Standards
- Testing methods
-