Safety factor
Safety Factor (SF) or Factor of Safety (FoS) is generally defined by industry rather than manufacturer. It may be significantly different to Design Factor (DF). For example, a particular connector may have an MBS of 50kN, a manufacturer specified DF of 4, but an industry specified SF of 10 when used for a particular application.
The Design Factor (DF) is specified by a designer or manufacturer, and this defines the factor applied to the MBS to determine maximum load acceptable load for a component in normal use.
The Factor of Safety for a roping system is a ratio which describes the margin of safety between the operating load and the load at which the system will fail.
Safety factor is often misunderstood and a typical conversation between a safety officer and a rope technician might go something like this:
– Hey, nice system you have got there. How much are you expecting to lift?
– Thanks. Two people, so I guess around 300kg worst case.
– Ok, so a 3kN load. What is your Factor of Safety?
– 10:1
– Great, thanks.
This image shows a standard 2-rope descent system.

If we assume 100kN anchors, 30kN ropes, 24kN carabiners, and that knots halve the rope MBS (50%), then we can see that the weakest link in this system will be one of the knotted ropes at 30kN x 50% = 15kN.
The maximum anticipated force for this system will be the maximum allowable for a backup device – which is 6kN.
Thus, the Factor of Safety for this system is 15kN / 6kN = 2.5
Notice that I have had no need to use terms like ‘static’ or ‘dynamic’. A Factor of Safety is simply that of the system under foreseeable loadings.
Consider the following simple system
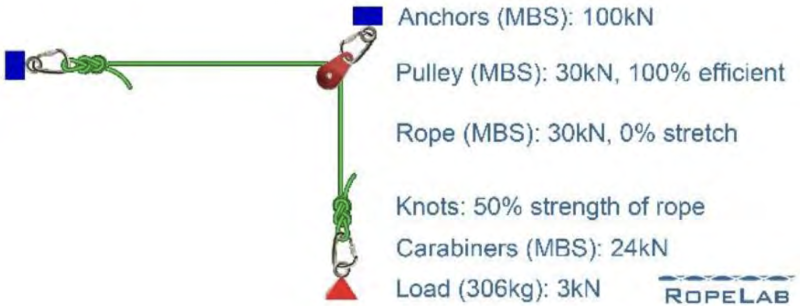
Given the stated conditions, our goal is to determine the Factor of Safety for the system. The system is static (nothing is moving) so we can go through each component and calculate the individual safety factors.
Rope
The tension in the rope will be 3kN however the 30kN rope with the knots (50%) will be reduced to 15kN. Thus, for the rope,
SF = 15kN / 3kN = 5
Carabiners (at the load and the main anchor)
SF = 24kN / 3kN = 8
Main anchor
SF = 100kN / 3kN = 33.3
It is a little more difficult to work out for the pulley and the carabiner and anchor to which it is attached. This pulley redirects the 3kN rope through 90degrees. Vector addition will show us that the load on the pulley will be 1.41 times greater than the tension in the rope. So the effective load on the pulley will be 3kN x 1.41 = 4.23kN.
Pulley
SF = 30kN / 4.23kN = 7.09
Carabiner (on pulley)
SF = 24kN / 4.23 = 5.67
Anchor (on pulley)
SF = 100kN / 4.23 = 23.64
Now we can look at these calculated Safety Factors and see that the SF of the weakest link is one of the knots in the rope.
Thus, the Factor of Safety for this system is 5
At the time of creation of NFPA (The National Fire Protection Association) 1983, 10:1 safety factors were commonly observed in many other industries, but the NFPA committee pushed to have that requirement raised to 15:1 specifically for ropes. The most plausible explanation for this is because knots placed in a rope reduce its strength by around 1/3, reducing 15 by 1/3 would still maintain a 10:1 safety ratio.
The 7th edition (2017) sought to clarify the definitions around General-Use equipment and Technical-Use.
NFPA 1983 calculates the 15:1 safety factor by using a 300 lb load for each rescuer or patient on the rope system. Rope and software meeting the General-Use category is therefore capable of supporting a 2-person load (ie: 600 lbs):
2 x 300 lbs x 15:1 safety = 9,000 lbs (roughly 40 kN)
Rope and software meeting the Technical-Use category is able to support a 1-person load (ie: 300 lbs):
1 x 300 lbs x 15:1 safety = 4,500 lbs (roughly 20 kN)
You might notice that some rescue hardware items, like carabiners, meet and exceed this 40 kN requirement, while other hardware pieces, like pulleys and descent control devices may not. Why so? Unfortunately there is no satisfactory answer. What is clear is that the Technical Committee that writes the 1983 Standard groups different types of equipment differently:
- Ropes and software need to meet the 40 kN requirement for General-Use and 22 kN for Technical-Use;
- Carabiners need 40 kN (G) as well along with a minimum 11 kN strength on the minor axis or with the gate open (22 kN for Technical-Use with 7 kN minor axis or gate open);
- Pulleys only need 36 kN (G) and 22 kN strength for the becket (18 kN and 11 kN respectively for the Technical-Use designation);
- Portable anchors also need the same 36 kN (G) or 18 kN (T) strength;
Words such as 15:1, one-person rope, two-person rope, safety factors, and many similar such sentiments, last time appeared in NFPA 1983 in the 1995 Edition. So, nowadays there are no prescribed ratios or loads. You, my friends and colleagues, are the Authority Having Jurisdiction. 1983 just informs manufacturers how strong to create and design the equipment, how to test it and how to label it. Your team and your department get to do the homework and select the gear and load limits that meet your needs. In the eyes of this document, there are no imposed limits on the loads you use with Technical Use gear. The NFPA does not impose a safety factor on your equipment or team’s systems. A one-person load has no set value. Your team is responsible for setting this value.
It gives me great satisfaction to conclude that 15:1 is not really very important anymore. It is real and part of our rescue history—our early foundations and identity. As a rescue community, it is important to remember who we are and where we came from. Now is the time for our community to look forward and solve more difficult problems. The cliché arguments about absolute breaking strength and two-person loads is so 1995.
Physics for roping technicians (2022)
Ask a Pro: How did the NFPA come up with a 15:1 safety factor? (2020)



